Rumus Hukum II Kirchhoff dan Contohnya

Rumus Hukum II Kirchhoff dan Contohnya

Rumus Hukum II Kirchhoff  - Hukum II Kirchhoff atau hukum loop menyatakan bahwa jumlah perubahan potensial yang mengelilingi lintasan tertutup pada suatu rangkaian harus sama dengan nol. Hukum ini di dasarkan pada hukum kekekalan energi.

Secara matematis hukum II Kirchhoff dapat dinyatakan sebagai berikut.  

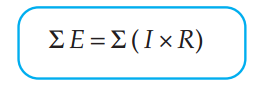Rumus Hukum II Kirchhoff 

Keterangan:E : ggl sumber arus (volt)I : kuat arus (A)R : hambatan (Ω ) (Ω dibaca OHM)

Pada perumusan hukum II Kirchhoff, mengikuti ketentuan sebagai berikut.
a. Semua hambatan (R) dihitung positif.
b. Pada arah perjalanan atau penelusuran rangkaian tertutup (loop), jika sumber arus berawal dari kutub negatif ke kutup positif, maka gglnya dihitung positif. Jika sebaliknya dari kutub positif ke kutub negatif, maka ggl nya dihitung negatif.  

Tanda positif dan negatif ggl  

(Baca juga Elemen GGL)

c. Arus yang searah dengan penelusuran loop dihitung positif, sedang yang berlawanan dengan arah penelusuran dihitung negatif.
d. Jika hasil akhir perhitungan kuat arus bernilai negatif, maka kuat arus yang sebenarnya merupakan kebalikan dari arah yang ditetapkan  

Rumus Hukum II Kirchhoff 

a. Kuat Arus Listrik dalam Rangkaian Sederhana  

Pada dasarnya sumber tegangan ggl memiliki hambatan dalam yang disimbulkan dengan r. Nilai r ini adalah nilai hambatan yang ada dalam ggl sumber tegangan pada suatu rangkaian. Perhatikan

Gambar di bawah ini:

Rangkaian tertutup  

Pada gambar tersebut melukiskan rangkaian tertutup yang terdiri atas sebuah sumbu arus dengan ggl E, hambatan dalam r, dan sebuah penghambat dengan hambatan R, sedang arus pada rangkaian I. Menurut hukum II Kirchhoff, pada rangkaian berlaku persamaan seperti berikut. 

hukum II Kirchhoff  

Keterangan:E : ggl sumber arus (V)I : kuat arus (A)r : hambatan dalam sumber arus ( Ω )R : hambatan penghambat ( Ω ) 

Nilai I × R pada persamaan di atas merupakan tegangan penggunaan di luar sumber arus yang disebut tegangan jepit (K). Jadi, persamaan di atas dapat ditulis sebagai berikut. 

Keterangan:K : tegangan jepit (V)  

Contoh Soal Hukum Kirchhoff

Sebuah kawat penghantar dengan hambatan 11,5 ohm dihubungkan dengan sumber tegangan 6 V yang hambatan dalamnya 0,5 ohm.

Hitunglah kuat arus pada rangkaian dan tegangan jepitnya!
Diketahui : 

a. R : 11,5 Ωb. E : 6 V
c. r = 0,5 Ω

Ditanyakan: 

a. I = ...?
b. K = ...?

Jawab :

b. Kuat Arus Listrik dalam Rangkaian Majemuk (Kompleks)  

Gambar di bawah ini menunjukkan satu rangkaian tertutup yang terdiri atas satu loop. Misalkan arah arus dan arah penelusuran loop kita tentukan searah putaran jarum jam. Menurut hukum II Kirchhoff pada rangkaian berlaku persamaan ∑E = ∑(I × R) . Oleh karena itu persamaannya menjadi seperti berikut.  

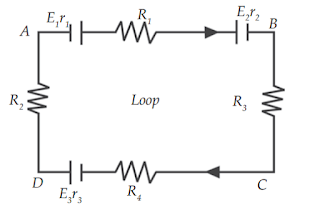Rangkaian satu loop.  

Jika pada penjabaran di atas dihasilkan nilai I negatif, maka arah arus yang sebenarnya adalah kebalikan dari arah yang ditentukan pada gambar. Bagaimana jika penelusuran rangkaian berawal dari satu titik dan berakhir pada titik lain? Misalkan Anda akan menentukan tegangan atau beda potensial antara titik A dan B pada Gambar di atas. Berdasarkan Hukum II Kirchhoff dapat dihitung dengan persamaan berikut  

Untuk rangkaian yang memiliki dua loop atau lebih dapat diselesaikan dengan hukum II Kirchhoff dan hukum I Kirchhoff. Perhatikan Gambar di bawah ini!

Pada gambar di atas dilukiskan rangkaian tertutup yang terdiri atas dua loop. Arah arus dan arah penelusuran tiap loop. Misalkan Anda bagi menjadi seperti berikut.  

Contoh Soal Hukum Kirchof dengan Loop

Diketahui : 

a. E1 = 8 V
b. R1 = 4 Ωc. E2 = 18 V
d. R2 = 2 Ωe. R3 = 6 Ω

Ditanyakan: 

a. I1 = ...?
b. I2 = ...?
c. I3 = ...?  

Jawab:  

Nilai I1, Anda masukkan ke persamaan (2) 

8 = 10 I1 + 6 I2

8 = 10 (–1) + 6 I2I2 = 3 A
Nilai I2, Anda masukkan pada persamaan (1)I3 = I1 + I2= –1 + 3
= 2I1 negatif, berarti I berlawanan dengan arah yang telah ditentukan.

Ada pertanyaan mengenai Rumus Hukum II Kirchhoff dan Contohnya ini? Silahkan kunjungi fanspage di FB Garda Pengetahuan.